Category Archives: DataViz

C#: Tumblr Blog Description Top Word Frequency List Visualization

Leave a reply

Browsing reddit; I found a parsed dataset from Tublr. Link Here.
I used code from an older post to obtain a list of unique words, and their frequencies.
Next, I used a default TermCloud – Sample from GoogleCharts’s Additional Charts Gallery, to generate this image in a web browser.

Tublr blog description: words with a frequency greater than 5,000, ordered by most to least frequent.
FINAL_TUBLR_WORDFREQ

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.IO;
 
namespace ordertumblrwords
{
    class Program
    {
        static void Main(string[] args)
        {
            int counter = 0;
            string line;
            Dictionary<string, int> hashfreq = new Dictionary<string, int>();
            System.IO.StreamReader file =
               new System.IO.StreamReader("C:\\Book\\New folder\\OUTPUT.txt");
            while ((line = file.ReadLine()) != null)
            {
                string[] parts = line.Split(':');
                int freq = int.Parse(parts[1].ToString().Trim());
                hashfreq.Add(parts[0], freq);
                counter++;
            }
            file.Close();
            int q = 0;
            string masterstring = "";
            foreach (KeyValuePair<string, int> item in hashfreq.OrderByDescending(key => key.Value))
            {
                if (item.Value > 5000)
                {
                    Console.WriteLine("data.setValue(" + q + ", 0, '" + item.Key + "');");
                    Console.WriteLine("data.setValue(" + q + ", 1, "+item.Value+");");
                    q += 1;
                    masterstring += "data.setValue(" + q + ", 0, '" + item.Key + "');\r\n";
                    masterstring += "data.setValue(" + q + ", 1, " + item.Value + ");\r\n";
                }
 
            }
            StreamWriter streamWrite;
            streamWrite = File.AppendText("C:\\Book\\MANTASMAIN.txt");
            streamWrite.WriteLine(masterstring);
            streamWrite.Close();
        }
    }
}

Visualizing Project Euler Problem 58 using Processing/Java

Leave a reply

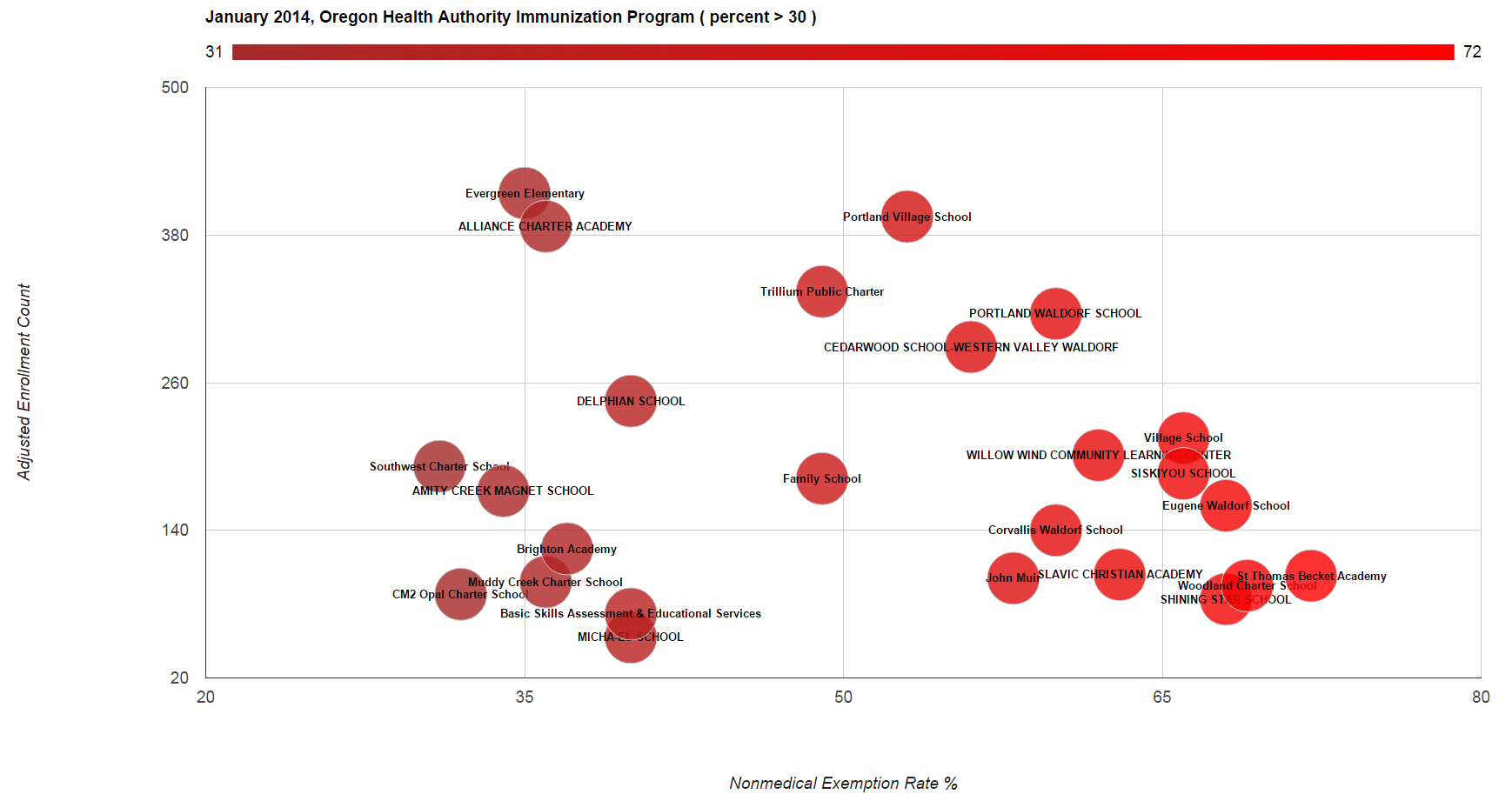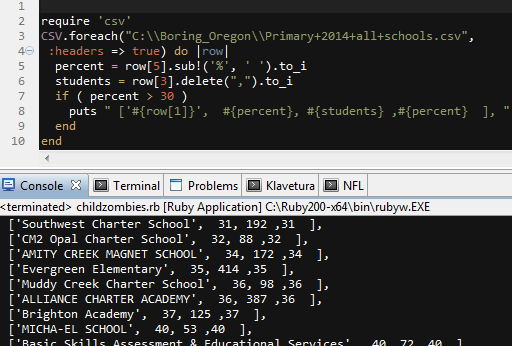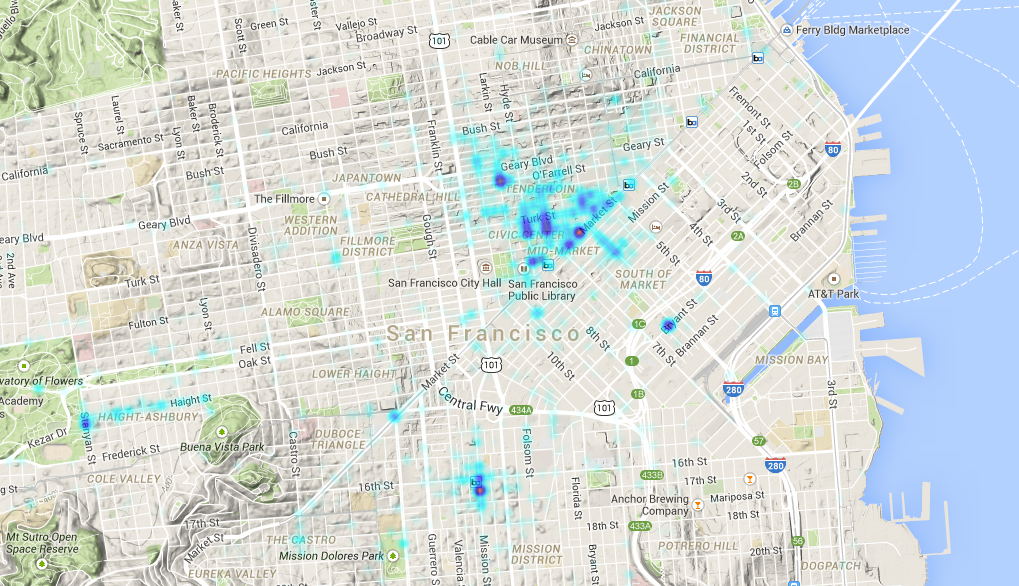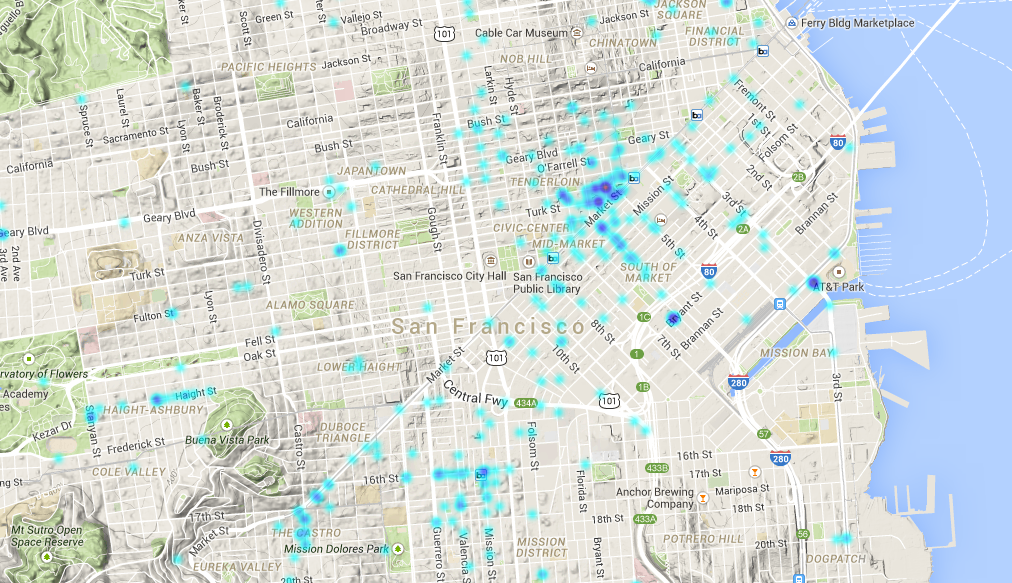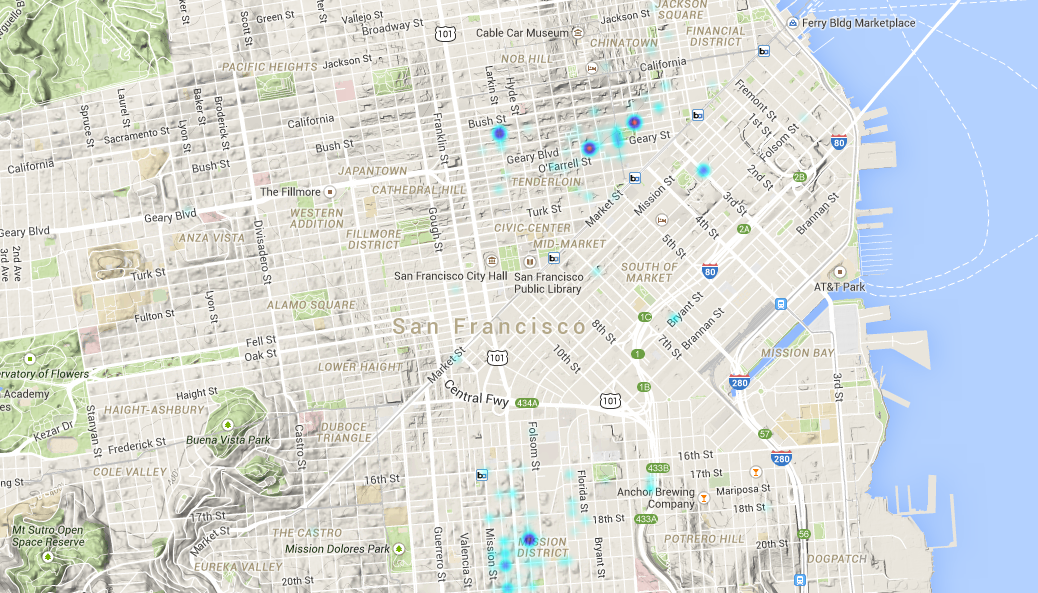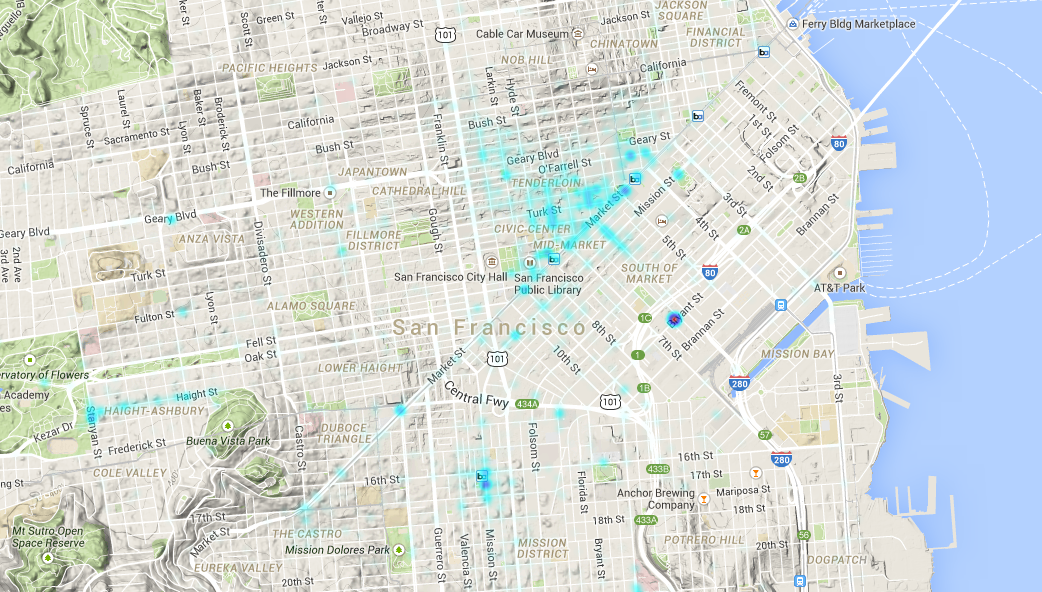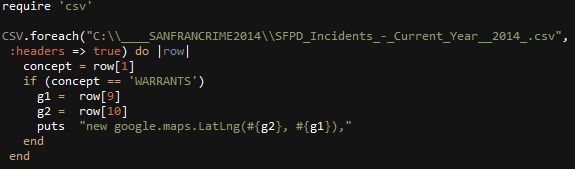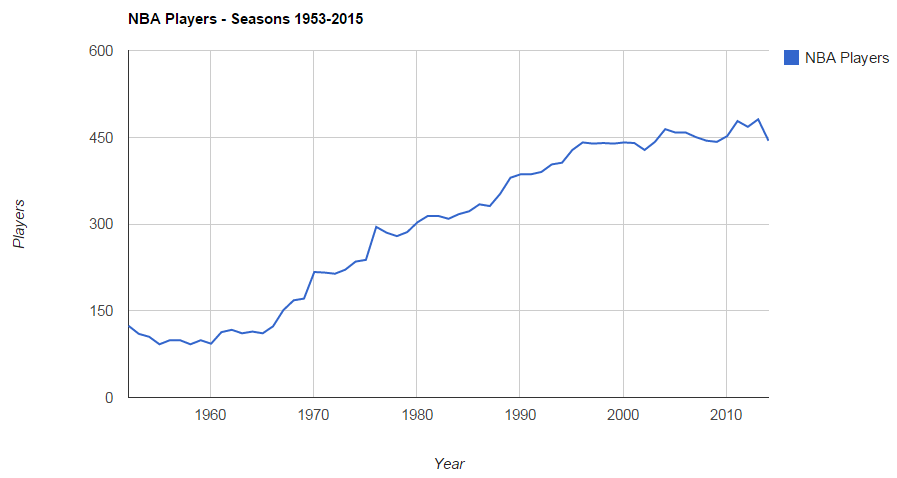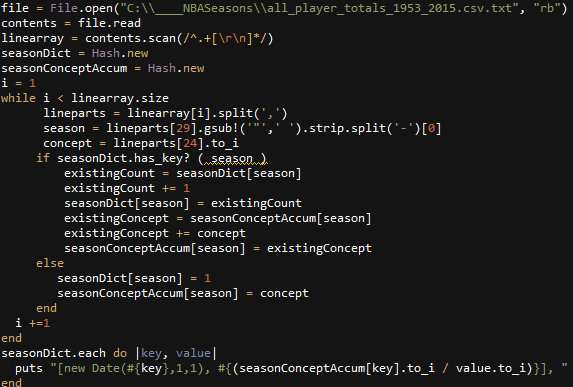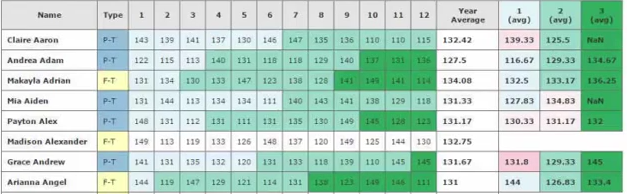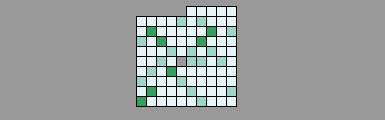
spiralprime2

Another visualization of Euler 58. This time, using Processing with Java.
Previous .NET winforms visualization of Euler 58
https://projecteuler.net/problem=58

primekey

spirialprimes

public int i_x = 500;
public int i_y = 500;
public static int Current_Direction = 0;
public int cur_step = 1;
public int skip_at = 7;
public int skip = 3;
public boolean first_turn = false;
public int count = 5;
public int diag_count = 4;
public int prime_count = 2;
 
void setup()
{
  size(1000, 1000);
  background(153);
}
 
void draw(){
  cur_step += 1;
  if ( isPrime(cur_step))
  {
    if (cur_step == skip_at)
    {
      fill(44,162,95);
    }
    else
    {
      fill(153,216,201);
    }
  }
  else
  {
    fill(229,245,249);
  }
 
  if (Current_Direction == 0)
  {
     rect( i_x + 10, i_y, 10, 10);
      i_x += 10;
  }
  else if (Current_Direction == 3)
  {
      rect( i_x, i_y + 10, 10, 10);
      i_y += 10;
  }
  else if (Current_Direction == 2)
  {
      rect( i_x - 10, i_y, 10, 10);
      i_x -= 10;
  }
  else if (Current_Direction == 1)
  {
      rect( i_x, i_y - 10, 10, 10);
      i_y -= 10;
  }
 
  if (cur_step &lt;= 3)
      Turn();
  if (cur_step == 5)//2
      Turn();
  if (skip_at == cur_step)
  {
      skip_at += skip;
      if (first_turn == false)
          first_turn = true;
      else
      {
          first_turn = false;
          skip += 1;
      }
      Turn();
  }
}
 
protected void Turn()
{
    if (Current_Direction == 3)
        Current_Direction = 0;
    else
        Current_Direction += 1;
}
 
public boolean isPrime(int n)
{
  if (n == 1)
        return false;
    if (n == 2)
        return true;
    for (int i = 2; i &lt; n; ++i)
    {
        if ((n % i) == 0)
            return false;
    }
 return true; 
}

pROCESSINGlEARNING
A fun little project whilst attempting to learn https://processing.org/

I draw 10 x 10 pixel boxes, 100 per row. If the number is a Prime, I highlight it in orange.

100X100PRIMES

Java

//Number Counter
public int i_num = 0;
//Draw Coordinates
public int i_x = 0;
public int i_y = 0;
 
void setup()
{
  size(1000, 1000);
  background(153);
}
 
void draw(){
 
      if ( isPrime(i_num))
      {
        fill(204, 102, 0);
        rect(i_x*10,i_y + 0,10,10);
      }
      else
      {
        fill(255, 255, 255);
        rect(i_x*10,i_y + 0,10,10);
      }
  i_x +=1;
  i_num +=1;
 
  //Go to Next Line
  if ( i_x == 100 )
  {
    i_x = 0;
    i_y += 10; 
  }
 
}
 
public boolean isPrime(int n)
{
  if (n == 1)
        return false;
    if (n == 2)
        return true;
    for (int i = 2; i &lt; n; ++i)
    {
        if ((n % i) == 0)
            return false;
    }
 return true; 
}

Visualizing Project Euler Problem 15 using C# Winforms | Lattice Paths

1 Reply

Mapping paths..

public static Brush aBrush = (Brush)Brushes.Black;
public static string path_collect = "";
public static LinkedList<string> complete_paths = new LinkedList<string>();
public bool wall = false;
public bool floor = false;
 
public static int miliseconds = 15;
 
public int current_x = 10;
public int current_y = 10;
 
 
public Form1()
{
    InitializeComponent();
}
 
 
private void Form1_Load(object sender, EventArgs e)
{
    label3.Text = miliseconds + "ms";
}
 
private void Form1_Paint(object sender, PaintEventArgs e)
{
    int x = 10;
    int y = 10;
    for (int i = 1; i < 21; i++)
    {
        for (int j = 1; j < 21; j++)
        {
            e.Graphics.DrawEllipse(Pens.Black, x* i , y *j, 6, 6);
        }
    }
}
 
private void bntPath_Click(object sender, EventArgs e)
{
    bntPath.Enabled = false;
    backgroundWorker1.RunWorkerAsync();
}
 
 
protected void Move(string path)
{
    Graphics g = this.CreateGraphics();
 
    foreach (char c in path)
    {
        if (c == '0')
        {
            g.FillRectangle(aBrush, current_x + 10, current_y, 10, 10);
            current_x += 10;
            path_collect += "→";
        }
        else if (c == '1')
        {
            g.FillRectangle(aBrush, current_x, current_y + 10, 10, 10);
            current_y += 10;
            path_collect += "↓";
        }
    }
 
    current_x = 10;
    current_y = 10;
 
    label2.Text = "New Unique Path\r\n" + path_collect;
 
    Brush NewBrush = new SolidBrush(GetRandomColor());
    aBrush = NewBrush;
    path_collect = "";
 
}
 
 
private void backgroundWorker1_DoWork_1(object sender, DoWorkEventArgs e)
{
    /*
    while (true) 
    {
        MoveRandom();
        Thread.Sleep(miliseconds);
    }
        */
    Int64 i = 0;
    Int64 count_unique_paths = 0;
 
 
    while (true)
    {
        string bits = Convert.ToString(i, 2).PadLeft(38, '0');
        string check = bits;
        check = Regex.Replace(check, "0", "");
        if (check.Length == 19)
        {
            Move(bits);
            //Thread.Sleep(50);
            count_unique_paths += 1;
            label4.Text = "Distinct Paths " + count_unique_paths;
        }
        i += 1;
    }
 
}
 
string row = "";
 
public bool completerow = true;
 
private Random random;
private Color GetRandomColor()
{
    random = new Random();
    return Color.FromArgb(random.Next(0, 255), random.Next(0, 255), random.Next(0, 255));
}
 
protected void MoveRandom()
{
    Graphics g = this.CreateGraphics();
    Random rand = new Random();
    int random = rand.Next(0, 2);
 
    if (random == 0)
    {
        if (!wall)
        {
            g.FillRectangle(aBrush, current_x + 10, current_y, 10, 10);
            current_x += 10;
            path_collect += "→";
        }
    }
    else if (random == 1)
    {
        if (!floor)
        {
            g.FillRectangle(aBrush, current_x, current_y + 10, 10, 10);
            current_y += 10;
            path_collect += "↓";
        }
    }
    CheckWall();
}
 
protected void CheckWall()
{
    if (current_x == 200)
        wall = true;
    if (current_y == 200)
        floor = true;
    if (wall && floor)
    {
        current_x = 10;
        current_y = 10;
        wall = false;
        floor = false;
        if (!complete_paths.Contains(path_collect))
        {
            complete_paths.AddLast(path_collect);
            label1.Text = "Complete " + complete_paths.Count;
            label2.Text = "New Unique Path\r\n" + path_collect;
 
        }
        Brush NewBrush = new SolidBrush(GetRandomColor());
        aBrush = NewBrush;
        path_collect = "";
    }
}

//Some fun with random paths at different speeds.
speed 50-1ms

Oregon’s Unvaccinated Children

Leave a reply

2014 Oregon Health Authority Immunization Program
Data found here

Y Axis Adjusted Enrollment Count
X Axis Nonmedical Exemption Rate %

OregonImmunizationProgram

Now let’s add some School Names to the tail ends of the chart above.
(Click on images for higher resolution)

Over 1,000 Enrolled and Nonmedical Exemption Rate % Greater than 3
School Names with over 3% percent of unvaccinated and have over one thousand students..
ImmunizedOver1000Over3percent

Nonmedical Exemption Rate Greater than 30 Percent
School Names with largest percentage of unvaccinated.
OregonOver30PercentNonimmune__

Ruby Example:
parsingOregon

Affordable Healthcare Act Compliance System Example

Leave a reply

mantascode promo

Random Empoloyees were created.
Random work hours for each month of 2014 were generated.
Random designations employment type attributed.
Random Measurement (start dates) associated.
6 Month look-back period.

ASP.net winforms was used to pull data from SQL Server.
C# was used to glue together an HTML table.
CSS was used to emphasize transitional employee types.