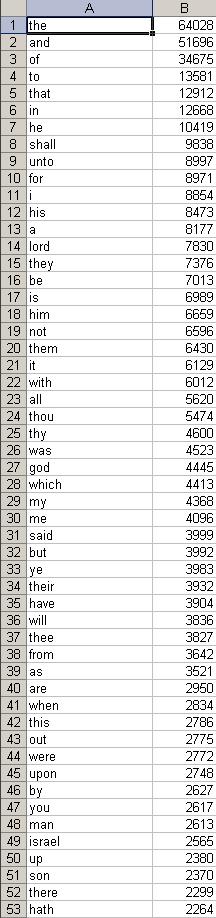
The book being parsed in this example is the King James Holy Bible bible.txt
Column A is the word, Column B is the frequency
download full output here
microsoft excel format : bibFreqxls.xls
xml format : bibFreqxml.txt
[csharp]
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.IO;
using System.Text.RegularExpressions;
using System.Collections;
namespace BibleWordFreq
{
class Program
{
static void Main(string[] args)
{
//create a stream reader
StreamReader bookStream;
//string of entire book
string fullBook=””;
//stream to file
bookStream = File.OpenText(“C:\\Book\\bible.txt”);
//read stream to string
fullBook = bookStream.ReadToEnd();
//close stream
bookStream.Close();
//remove numbers and punctuation
fullBook = Regex.Replace(fullBook, “\\.|;|:|,|[0-9]|'”, “”);
//create collection of words
MatchCollection wordCollection = Regex.Matches(fullBook, @”[\w]+”, RegexOptions.Multiline);
//create linked list for words
LinkedList<string> wordList = new LinkedList<string>();
//create hash table
Hashtable frequencyHash = new Hashtable();
//create linked list for unique words
LinkedList<string> uniqueWord = new LinkedList<string>();
//populate wordList with content of collection
for (int i = 0; i < wordCollection.Count; i++)
{
wordList.AddLast(wordCollection[i].ToString().ToLower().Trim());
}
//populate hashtable of word frequency
//for everyword in full word list
foreach (var word in wordList)
{
//if unique linked list does not contain a word, add it as a key, and set the value:1
//if unique linked list contains the word, increment the value
if (uniqueWord.Contains(word))
{
int wordCount = int.Parse(frequencyHash[word].ToString());
wordCount++;
frequencyHash[word] = wordCount;
}
else
{
uniqueWord.AddLast(word);
frequencyHash.Add(word, 1);
}
}
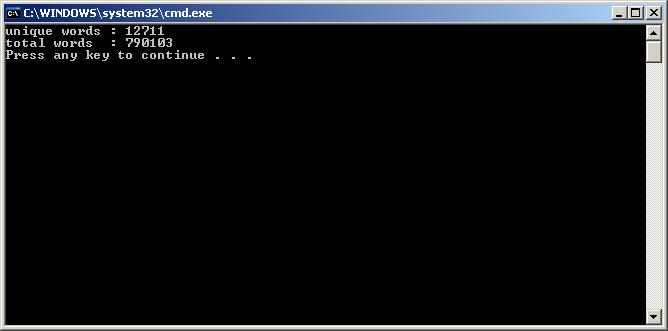
Console.WriteLine(“unique words : “+uniqueWord.Count);
Console.WriteLine(“total words : “+wordList.Count);
//create stream writer
StreamWriter streamWrite;
//create output file
streamWrite = File.AppendText(“C:\\Book\\OUTPUT.txt”);
//for each word+num in frequrncyHash
foreach (string word in frequencyHash.Keys)
{
//Write to file
streamWrite.WriteLine(string.Format(“{0}: {1}”, word, frequencyHash[word]));
}
streamWrite.Close();
}
}
}
[/csharp]


thanks very much this code help me to much in my GP .
This is very helpful coding. Can we optimize it using dictionary instead of linked list? Also I need to convert where ever non alphanumeric is there it should be treated as seperator. Can you suggest?
The following dictionary implementation is about 10 times faster:
using System;
using System.IO;
using System.Collections.Generic;
using System.Text.RegularExpressions;
namespace BibleWordFreq
{
class Program
{
static void Main(string[] args)
{
string fullBook = File.ReadAllText("C:\\Book\\bible.txt").ToLower();
//remove numbers and punctuation
fullBook = Regex.Replace(fullBook, "\\.|;|:|,|[0-9]|’", "");
//create collection of words
var wordCollection = Regex.Matches(fullBook, @"[\w]+");
//calculate word frequencies
var dict = new Dictionary();
for (int i = 0; i < wordCollection.Count; i++)
{
string word = wordCollection[i].Value;
if (!dict.ContainsKey(word))
dict[word] = 1;
else
++dict[word];
}
Console.WriteLine("unique words : " + dict.Count);
Console.WriteLine("total words : " + wordCollection.Count);
using (StreamWriter streamWrite = new StreamWriter("C:\\Book\\OUTPUT.txt"))
{
foreach (KeyValuePair kv in dict)
streamWrite.WriteLine("{0}: {1}", kv.Key, kv.Value);
}
}
}
}
Notice: The editor eats up Generic parameters (anything enclosed in angle brackets) even if surrounded by “code” tags. The dictionary should have string as key and int as value.
Hey how did you get the output in excel file, I did not find any code for that. Please help me with it.
Thanks
How many times is the words “present truth” found in the New King James Bible.