Category Archives: Euler

C# Project Euler Problem 954 Heptaphobia

A positive integer is called heptaphobic if it is not divisible by seven and no number divisible by seven can be produced by swapping two of its digits. Note that leading zeros are not allowed before or after the swap.

For example, 17 and 1305 are heptaphobic, but 14 and 132 are not because 14 and 231 are divisible by seven. Let C(N) count heptaphobic numbers smaller than N. You are given C(100) = 74 and C(10^4) = 3737.

Find C(10^13)

https://projecteuler.net/problem=954

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
 
namespace Heptaphobic_Super_Optimal
{
    internal class Program
    {
        static void Main(string[] args)
        {
 
            DateTime s_time = DateTime.Now;
 
            long max = 100;   // example upper bound
            long count = CountHeptaphobic(max);
 
 
            Console.WriteLine();
            Console.WriteLine();
            Console.WriteLine(max + " Heptaphobic count: " + count);
            Console.WriteLine();
            Console.WriteLine();
 
 
 
            Console.WriteLine();
            Console.WriteLine();
            DateTime e_time = DateTime.Now;
            Console.WriteLine("Duration   " + (e_time - s_time).TotalMinutes + " minutes");
            Console.WriteLine();
            Console.WriteLine();
            Console.WriteLine();
 
        }
 
 
        static long CountHeptaphobic(long max)
        {
            const int MaxDigits = 18;
            long[,] pow10Mod7 = new long[MaxDigits + 1, MaxDigits];
            for (int len = 1; len <= MaxDigits; len++)
            {
                pow10Mod7[len, len - 1] = 1;
                for (int i = len - 2; i >= 0; i--)
                    pow10Mod7[len, i] = (pow10Mod7[len, i + 1] * 10) % 7;
            }
 
            object lockObj = new object();
            long total = 0;
 
            Parallel.For(1L, max, () => 0L, (n, state, local) =>
            {
                if (IsHeptaphobicNumeric(n, pow10Mod7))
                    local++;
                return local;
            },
            local => { lock (lockObj) total += local; });
 
            return total;
        }
 
        static bool IsHeptaphobicNumeric(long num, long[,] pow10Mod7)
        {
            int[] digits = new int[18];
            int len = 0;
            long tmp = num;
            while (tmp > 0)
            {
                digits[len++] = (int)(tmp % 10);
                tmp /= 10;
            }
            Array.Reverse(digits, 0, len);
 
            long mod7 = 0;
            for (int i = 0; i < len; i++)
                mod7 = (mod7 + digits[i] * pow10Mod7[len, i]) % 7;
 
            if (mod7 == 0)
                return false;
 
            for (int i = 0; i < len; i++)
            {
                for (int j = i + 1; j < len; j++)
                {
                    if (i == 0 && digits[j] == 0)
                        continue;
 
                    long delta = ((digits[i] - digits[j]) * (pow10Mod7[len, j] - pow10Mod7[len, i])) % 7;
                    long newMod = (mod7 + delta + 7) % 7;
                    if (newMod == 0)
                        return false;
                }
            }
 
            return true;
        }
 
 
    }
}

C#: Euler 46

Leave a reply

EulerLEVEL2XXDD

Goldbach’s other conjecture

https://projecteuler.net/problem=46
It was proposed by Christian Goldbach that every odd composite number can be written as the sum of a prime and twice a square.

static void Main(string[] args)
{
    Console.BufferHeight = 8000;
    Console.WriteLine("Goldbach's other conjecture");
 
    for (int n = 3; n < 100000; n+=2)
    {
        if ( !isPrime(n) )
        {
            Console.WriteLine(n);
            bool works = false;
            while (!works)
            {
                for (int abc = 1; abc < 50; abc++)
                {
                    for (int j = 0; j < 10000; j++)
                    {
                        if (isPrime(j))
                        {
                            double check = j + (2 * Math.Pow(abc, 2));
                            if ((j + 2 * Math.Pow(abc,2)) > n)
                                break;
                            if (n == check)
                            {
//Console.WriteLine(n + " = " + j + " + 2*" + abc + "^2");
                                works = true;
                            }
                            if (works)
                                break;
                        }
                    }
                }
            }
            Console.WriteLine("----");
        }
    }
}
 
public static bool isPrime(int n)
{
    if (n == 1)
        return false;
    if (n == 2)
        return true;
    for (int i = 2; i < n; ++i)
    {
        if ((n % i) == 0)
            return false;
    }
    return true;
}

output
output

C#: Euler 36

Leave a reply

https://projecteuler.net/problem=36

The decimal number, 585 = 10010010012 (binary), is palindromic in both bases.
Find the sum of all numbers, less than one million, which are palindromic in base 10 and base 2.

//Euler 36
static void Main(string[] args)
{
    int num = 0;
    int sum = 0;
    while (num &lt; 1000000)
    {
        num += 1;
        string sBits = Convert.ToString(num, 2);
        string sNum = num.ToString();
        if (isSym(sNum) &amp;&amp; isSym(sBits))
        {
            sum += num;
        }
    }
    Console.WriteLine("Answer : "+sum);
}
 
public static string Reverse(string s)
{
    char[] charArray = s.ToCharArray();
    Array.Reverse(charArray);
    return new string(charArray);
}
 
public static bool isSym(string n)
{
    double half = n.Length / 2;
    string a  = n.ToString();
    string b  = n.ToString();
    b = Reverse(b);
    string new_a = "";
    string new_b = "";
    for (int i = 0; i &lt; half; i++)
    {
        new_a += a[i];
        new_b += b[i];
    }
    if (new_a == new_b)
        return true;
    return false;
}

Visualizing Project Euler Problem 15 using C# Winforms | Lattice Paths

1 Reply

Mapping paths..

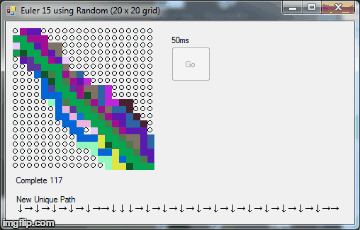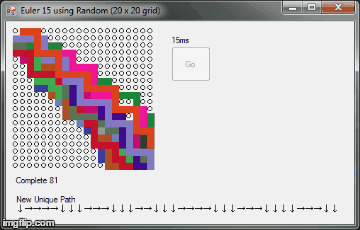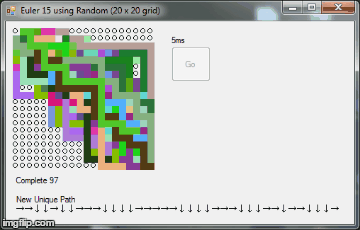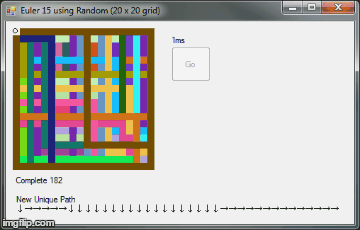
public static Brush aBrush = (Brush)Brushes.Black;
public static string path_collect = "";
public static LinkedList<string> complete_paths = new LinkedList<string>();
public bool wall = false;
public bool floor = false;
 
public static int miliseconds = 15;
 
public int current_x = 10;
public int current_y = 10;
 
 
public Form1()
{
    InitializeComponent();
}
 
 
private void Form1_Load(object sender, EventArgs e)
{
    label3.Text = miliseconds + "ms";
}
 
private void Form1_Paint(object sender, PaintEventArgs e)
{
    int x = 10;
    int y = 10;
    for (int i = 1; i < 21; i++)
    {
        for (int j = 1; j < 21; j++)
        {
            e.Graphics.DrawEllipse(Pens.Black, x* i , y *j, 6, 6);
        }
    }
}
 
private void bntPath_Click(object sender, EventArgs e)
{
    bntPath.Enabled = false;
    backgroundWorker1.RunWorkerAsync();
}
 
 
protected void Move(string path)
{
    Graphics g = this.CreateGraphics();
 
    foreach (char c in path)
    {
        if (c == '0')
        {
            g.FillRectangle(aBrush, current_x + 10, current_y, 10, 10);
            current_x += 10;
            path_collect += "→";
        }
        else if (c == '1')
        {
            g.FillRectangle(aBrush, current_x, current_y + 10, 10, 10);
            current_y += 10;
            path_collect += "↓";
        }
    }
 
    current_x = 10;
    current_y = 10;
 
    label2.Text = "New Unique Path\r\n" + path_collect;
 
    Brush NewBrush = new SolidBrush(GetRandomColor());
    aBrush = NewBrush;
    path_collect = "";
 
}
 
 
private void backgroundWorker1_DoWork_1(object sender, DoWorkEventArgs e)
{
    /*
    while (true) 
    {
        MoveRandom();
        Thread.Sleep(miliseconds);
    }
        */
    Int64 i = 0;
    Int64 count_unique_paths = 0;
 
 
    while (true)
    {
        string bits = Convert.ToString(i, 2).PadLeft(38, '0');
        string check = bits;
        check = Regex.Replace(check, "0", "");
        if (check.Length == 19)
        {
            Move(bits);
            //Thread.Sleep(50);
            count_unique_paths += 1;
            label4.Text = "Distinct Paths " + count_unique_paths;
        }
        i += 1;
    }
 
}
 
string row = "";
 
public bool completerow = true;
 
private Random random;
private Color GetRandomColor()
{
    random = new Random();
    return Color.FromArgb(random.Next(0, 255), random.Next(0, 255), random.Next(0, 255));
}
 
protected void MoveRandom()
{
    Graphics g = this.CreateGraphics();
    Random rand = new Random();
    int random = rand.Next(0, 2);
 
    if (random == 0)
    {
        if (!wall)
        {
            g.FillRectangle(aBrush, current_x + 10, current_y, 10, 10);
            current_x += 10;
            path_collect += "→";
        }
    }
    else if (random == 1)
    {
        if (!floor)
        {
            g.FillRectangle(aBrush, current_x, current_y + 10, 10, 10);
            current_y += 10;
            path_collect += "↓";
        }
    }
    CheckWall();
}
 
protected void CheckWall()
{
    if (current_x == 200)
        wall = true;
    if (current_y == 200)
        floor = true;
    if (wall && floor)
    {
        current_x = 10;
        current_y = 10;
        wall = false;
        floor = false;
        if (!complete_paths.Contains(path_collect))
        {
            complete_paths.AddLast(path_collect);
            label1.Text = "Complete " + complete_paths.Count;
            label2.Text = "New Unique Path\r\n" + path_collect;
 
        }
        Brush NewBrush = new SolidBrush(GetRandomColor());
        aBrush = NewBrush;
        path_collect = "";
    }
}

//Some fun with random paths at different speeds.
speed 50-1ms

Ruby: Project Euler Problem # 23

Leave a reply

http://projecteuler.net/problem=23

Non-abundant sums

A number n is called deficient if the sum of its proper divisors is less than n and it is called abundant if this sum exceeds n.

As 12 is the smallest abundant number, 1 + 2 + 3 + 4 + 6 = 16, the smallest number that can be written as the sum of two abundant numbers is 24. By mathematical analysis, it can be shown that all integers greater than 28123 can be written as the sum of two abundant numbers. However, this upper limit cannot be reduced any further by analysis even though it is known that the greatest number that cannot be expressed as the sum of two abundant numbers is less than this limit.

Find the sum of all the positive integers which cannot be written as the sum of two abundant numbers.

Ruby_Euler_23