In this tutorial I will show you how to iterate through a website using a WebClient, Save each page’s content into a string, parse it using regular expressions, and save it as XML.
I will be parsing airplane data from airliners.net
Here is a picture of what the website looks like.
Get started with a .NET C# Console application and create a WebClient.
Use the URL and Output the html returned.
WebClient wc = new WebClient(); string htmlString = wc.DownloadString("http://www.airliners.net/aircraft-data/stats.main?id=2"); Console.WriteLine(htmlString); |
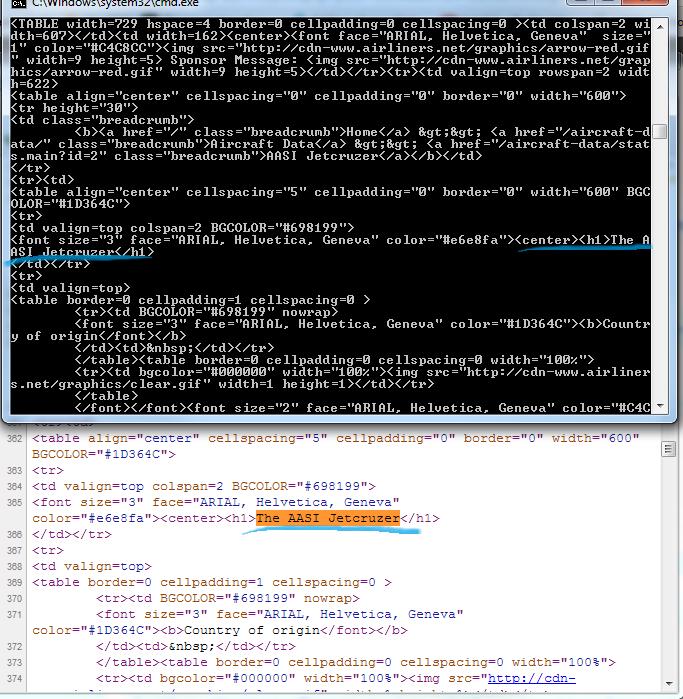
Lets take a look at both the console output and the source of the page to make sure we got the right html back.
Console and Page Source
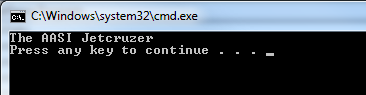
Success, we found the Airplane title! Now lets see if we can parse it, and only it, from the entire string of html.
Try to see if there is a pattern that’s unique to what you need.
![]()
WebClient wc = new WebClient(); string htmlString = wc.DownloadString("http://www.airliners.net/aircraft-data/stats.main?id=2"); Match mTitle = Regex.Match(htmlString, @"<center><h1>(.*?)</h1>"); if (mTitle.Success) { string airplaneTitle = mTitle.Groups[1].Value; Console.WriteLine(airplaneTitle); } |
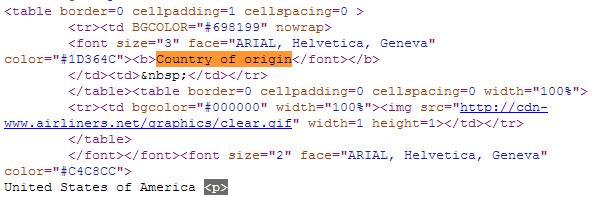
Now lets get Country of Origin and the other categories.
string airplaneCountry = ""; Match mCountry = Regex.Match(htmlString, @"<b>Country of origin</font>(.*?)<p>", RegexOptions.Singleline); if (mCountry.Success) { airplaneCountry = mCountry.Groups[1].Value; Console.WriteLine(airplaneCountry); } Console.WriteLine("***************************************************************"); //manicure the pattern string //Replace everything before the last (greater than) sign with and empty string airplaneCountry = Regex.Replace(airplaneCountry, "(.*?)>", "").Trim(); Console.WriteLine(airplaneCountry); |
Now I am tired of typing, so lets make a method for everything else.
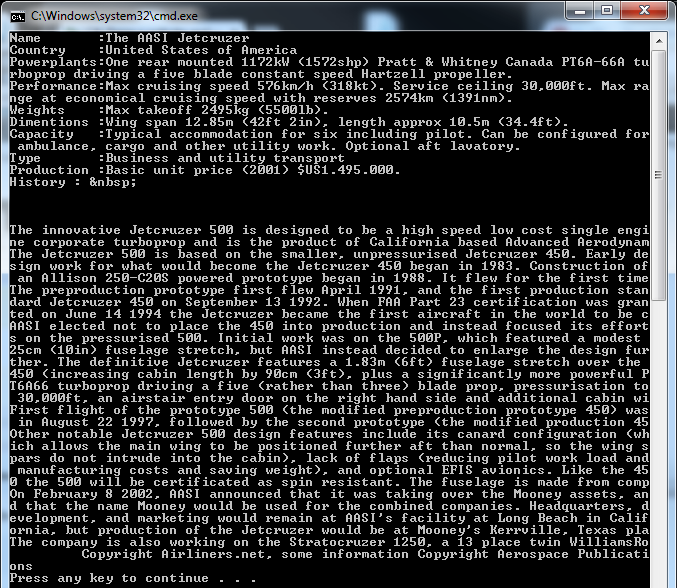
static void Main(string[] args) { WebClient wc = new WebClient(); string htmlString = wc.DownloadString("http://www.airliners.net/aircraft-data/stats.main?id=2"); Console.WriteLine("Name :"+ parsePattern(@"<center><h1>(.*?)</h1>",htmlString)); Console.WriteLine("Country :" + parsePattern(@"<b>Country of origin</font>(.*?)<p>", htmlString)); Console.WriteLine("Powerplants:" + parsePattern(@"<b>Powerplants</font>(.*?)<p>", htmlString)); Console.WriteLine("Performance:" + parsePattern(@"<b>Performance</font>(.*?)<p>", htmlString)); Console.WriteLine("Weights :" + parsePattern(@"<b>Weights</font>(.*?)<p>", htmlString)); Console.WriteLine("Dimentions :" + parsePattern(@"<b>Dimensions</font>(.*?)<p>", htmlString)); Console.WriteLine("Capacity :" + parsePattern(@"<b>Capacity</font>(.*?)<p>", htmlString)); Console.WriteLine("Type :" + parsePattern(@"<b>Type</font>(.*?)<p>", htmlString)); Console.WriteLine("Production :" + parsePattern(@"<b>Production</font>(.*?)<p>", htmlString)); //lol :D Damn this History! //Console.WriteLine(parsePattern(@"<b>History</font>(.*?)<table border=0 cellpadding=1 cellspacing=0 >", htmlString)); //History breaks my method pattern cause there's too many <p>'s //Doing History Manually, Due to Different Pattern. Match mHistory = Regex.Match(htmlString, @"<b>History</font>(.*?)<table border=0 cellpadding=1 cellspacing=0 >", RegexOptions.Singleline); if (mHistory.Success) { string strContent = mHistory.Groups[1].Value; //Google your problems "C# regex to remove html" - thanks stackoverflow //Get @"<[^>]*>" strContent = Regex.Replace(strContent, @"<[^>]*>", "").Trim(); Console.WriteLine("History : " + strContent); } } |
public static string parsePattern(string pat, string htmlString) { Match mCategory = Regex.Match(htmlString, @pat, RegexOptions.Singleline); if (mCategory.Success) { string strContent = mCategory.Groups[1].Value; if (strContent.Contains('>')) { strContent = Regex.Replace(strContent, "(.*?)>", "").Trim(); return strContent; } else return strContent; } return ""; } |
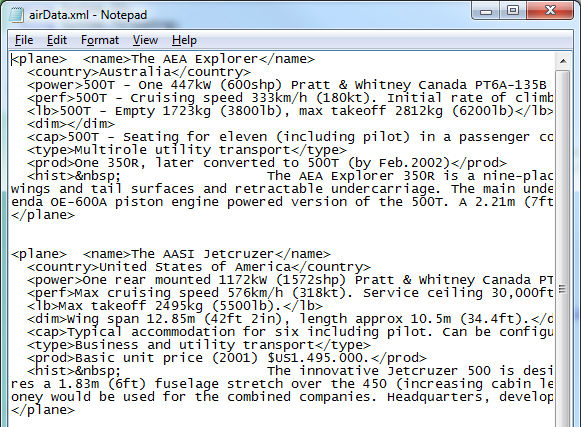
Now lets save everything into xml :D
I Created a Folder in my C: Drive called C:\Airplanes\
Iterate through each page and save the content.
Here’s the full Code to do the Whole Website:
static void Main(string[] args) { //Since we don't want to hold a glock up to the webserver's dome piece: //Let's pretend to be a human who goes to each page within 1 - 3 seconds randomly. WebClient wc = new WebClient(); int pageCount = 1; int randomWait = 0; Random random = new Random(); while (true) { randomWait = random.Next(1000, 3000); Thread.Sleep(randomWait); string htmlString = wc.DownloadString("http://www.airliners.net/aircraft-data/stats.main?id=" + pageCount); ReadAndAppend(htmlString); pageCount++; Console.WriteLine("Saving :" + pageCount); } } public static void ReadAndAppend(string htmlString) { string name = parsePattern(@"<center><h1>(.*?)</h1>", htmlString); string country = parsePattern(@"<b>Country of origin</font>(.*?)<p>", htmlString); string power = parsePattern(@"<b>Powerplants</font>(.*?)<p>", htmlString); string perf = parsePattern(@"<b>Performance</font>(.*?)<p>", htmlString); string lb = parsePattern(@"<b>Weights</font>(.*?)<p>", htmlString); string dim = parsePattern(@"<b>Dimensions</font>(.*?)<p>", htmlString); string cap = parsePattern(@"<b>Capacity</font>(.*?)<p>", htmlString); string type = parsePattern(@"<b>Type</font>(.*?)<p>", htmlString); string prod = parsePattern(@"<b>Production</font>(.*?)<p>", htmlString); string hist = ""; Match mHistory = Regex.Match(htmlString, @"<b>History</font>(.*?)<table border=0 cellpadding=1 cellspacing=0 >", RegexOptions.Singleline); if (mHistory.Success) { string strContent = mHistory.Groups[1].Value; strContent = Regex.Replace(strContent, @"<[^>]*>", "").Trim(); hist = strContent; } //make the xml string xmlString = "<plane>"; xmlString += " <name>" + name + "</name>\r\n"; xmlString += " <country>" + country + "</country>\r\n"; xmlString += " <power>" + power + "</power>\r\n"; xmlString += " <perf>" + perf + "</perf>\r\n"; xmlString += " <lb>" + lb + "</lb>\r\n"; xmlString += " <dim>" + dim + "</dim>\r\n"; xmlString += " <cap>" + cap + "</cap>\r\n"; xmlString += " <type>" + type + "</type>\r\n"; xmlString += " <prod>" + prod + "</prod>\r\n"; xmlString += " <hist>" + hist + "</hist>\r\n"; xmlString += "</plane>\r\n\r\n"; //Show me the saves and count Console.WriteLine(xmlString); //save to C:\Airplanes\ StreamWriter streamWrite; streamWrite = File.AppendText("C:\\Airplanes\\airData.xml"); streamWrite.WriteLine(xmlString); streamWrite.Close(); } public static string parsePattern(string pat, string htmlString) { Match mCategory = Regex.Match(htmlString, @pat, RegexOptions.Singleline); if (mCategory.Success) { string strContent = mCategory.Groups[1].Value; if (strContent.Contains('>')) { strContent = Regex.Replace(strContent, "(.*?)>", "").Trim(); return strContent; } else return strContent; } return ""; } |