http://projecteuler.net/problem=53
Combinatoric selections
There are exactly ten ways of selecting three from five, 12345:
123, 124, 125, 134, 135, 145, 234, 235, 245, and 345
In combinatorics, we use the notation, 5C3 = 10.
where r n, n! = n(n1)…321, and 0! = 1.How many, not necessarily distinct, values of nCr, for 1
n
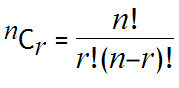
Does this count as solution a for this problem?
value = 12345
result = value.to_s.scan(/.{1,1}/).combination(3).to_a.map { |e| e.join.to_i }
p result
Partially, yes.