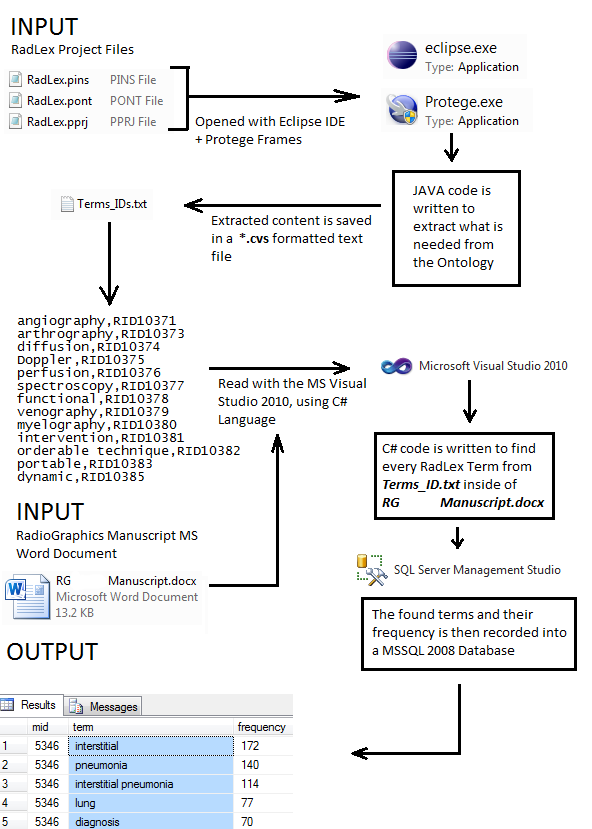
How to loop over a list of numeric IDs within the URL, using C#.
Some websites use numeric identifiers in order to retrieve and display information about a parictular product, article, service, or whatever.
So if you see a URL which ends in, or contains something like this:
http://www.example.com/products/product_detail.aspx?id=12345
Chances are that the 12345 represents the identifier used to query a database and return formatted information (html) to your web browser.
So how can we get the returned html into a string?
simple!
WebClient myClient = new WebClient();
string sReturnedHtml = myClient.DownloadString
("http://www.example.com/products/product_detail.aspx?id=12345"); |
WebClient myClient = new WebClient();
string sReturnedHtml = myClient.DownloadString
("http://www.example.com/products/product_detail.aspx?id=12345");
That’s it. Now you probably want to apply some regular expressions to the returned html string, to do things like: remove tags, or parse specific chunks. (I know, I know, parsing html using regular expressions will make babies cry) Then, save it into your own XML or something.
I can’t show you how to parse chunks of the returned HTML in this example, because different websites will return their own unique html structures. But you can read more on how to parse the content of a string between two string fragments here C#: Parsing a string using Regular Expressions (Regex) (Just look for patterns surrounding what you need).
Here is how you would loop from ID 1 through ID 99999, and save the information for each id into a text file, with some tags to separating out each ID.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Net;
using System.Threading;
using System.IO;
namespace Simple_Spider
{
class Program
{
static void Main(string[] args)
{
for (int i = 1; i < 100000; i++)
{
//Use a try because some product ID's might not be public
//so even though they exist in the database, the website
//might not want to show them
try
{
Console.WriteLine("Parsing ID :" + i);
WebClient myClient = new WebClient();
string sReturnedHtml = myClient.DownloadString
("http://www.example.com/products/product_detail.aspx?id=" + i);
//Here is where you'd manipulate (sReturnedHtml)
//the returned string into your own structure
//or take out only what you need.
//Append your parsed content into a txt file
// inside directory C:\SPIDER\
StreamWriter streamWrite;
streamWrite = File.AppendText("C:\\SPIDER\\log.txt");
streamWrite.WriteLine
("<content id=\""+i+"\">\r\n"+sReturnedHtml+"\r\n </content>");
streamWrite.Close();
}
catch (Exception x)
{
//bad ID
Console.WriteLine("ERROR 404 maybe");
}
//This will pause the spider between each ID
//Make it sleep a second, so your not
//bombarding servers with requests
Thread.Sleep(1000);
}
}
}
} |
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Net;
using System.Threading;
using System.IO;
namespace Simple_Spider
{
class Program
{
static void Main(string[] args)
{
for (int i = 1; i < 100000; i++)
{
//Use a try because some product ID's might not be public
//so even though they exist in the database, the website
//might not want to show them
try
{
Console.WriteLine("Parsing ID :" + i);
WebClient myClient = new WebClient();
string sReturnedHtml = myClient.DownloadString
("http://www.example.com/products/product_detail.aspx?id=" + i);
//Here is where you'd manipulate (sReturnedHtml)
//the returned string into your own structure
//or take out only what you need.
//Append your parsed content into a txt file
// inside directory C:\SPIDER\
StreamWriter streamWrite;
streamWrite = File.AppendText("C:\\SPIDER\\log.txt");
streamWrite.WriteLine
("<content id=\""+i+"\">\r\n"+sReturnedHtml+"\r\n </content>");
streamWrite.Close();
}
catch (Exception x)
{
//bad ID
Console.WriteLine("ERROR 404 maybe");
}
//This will pause the spider between each ID
//Make it sleep a second, so your not
//bombarding servers with requests
Thread.Sleep(1000);
}
}
}
}